Month: May 2016

Heap

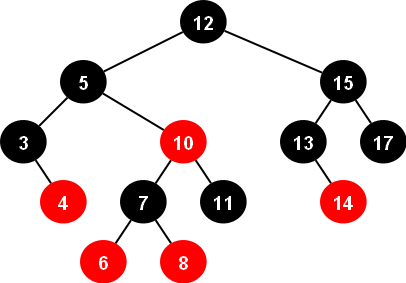
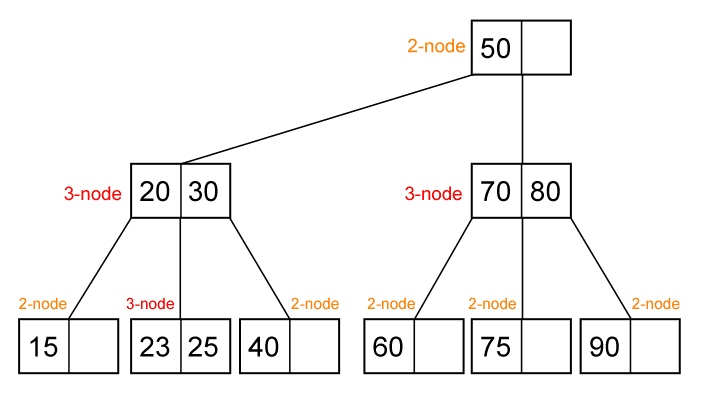
Heap Adalah struktur data yang berbentuk pohon yang memenuhi sifat-sifat heap yaitu jika B adalah anak dari A, maka nilai yang tersimpan di simpul A lebih besar atau sama dengan nilai yang tersimpan di simpul B.

Jenis-jenis dari heap adalah sebagai berikut:

Min–Heap

Heap dimana root memiliki nilai yang paling kecil dari keturunannya. Child dari node tersebut dan node seterusnya harus lebih besardari parent nya. Jika tidak memenuhi, maka dilakukan rotasi.

Max- Heap

Heap dimana root memiliki nilai yang paling besar. Child dari node tersebut dan node seterusnya harus lebih kecil dari parent nya. Jika tidak memenuhi, maka dilakukan rotasi.

Min-Max Heap

Complete Binary Tree yang dimana setiap level nya memiliki tingkatan heap berbeda (max dan min). Apabila root adalah level min, maka selanjutnya adalah level max, dst.

Insertion dalam Heap

Heap di insert satu persatu, dari atas, lalu kebawah. Dari kiri ke kanan terlebih dahulu secara berurutan ke index terakhir. Apabila heap tidak memenuhi syarat min/max/min-max heap maka dilakukan operasi up-heap.

Tries atau prefix tree adalah suatu pohon struktur data yang terurut yang menyimpan data array, biasanya string. Kata tries diambil dari kata RETRIEVAL, karena tries dapat menemukan kata tunggal dalam kamus dengan hanya awalan katanya saja.

Tries adalah suatu tree dimana setiap vertex/pathnya menggambarkan suatu kata, rootnya kosong

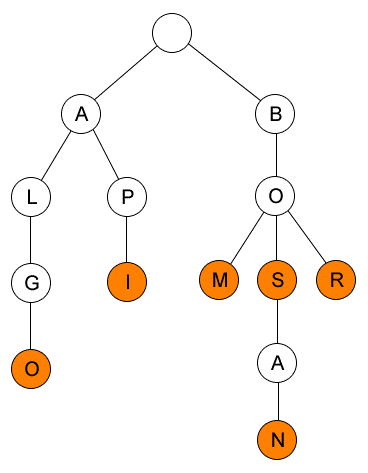Tree tersebut menunjukan kata : ALGO, API, BOM, BOS, BOSAN, BOR

Hashing

Hashing adalah transformasi dari string of character menjadi nilai yang lebih pendek atau key yang merepresentasikan suatu string aslinya.Hashing digunakan untuk mengindex dan retrieve item dalam database, karena akan lebih mudah menggunakan kata kunci yang lebih singkat dibandingkan string aslinya.

Hash Table
Hash table adalah tabel (array) yang menyimpan string aslinya.
Contoh Hash Table:

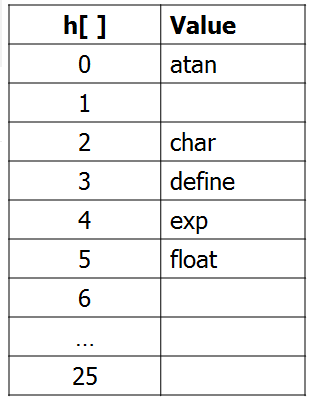
sumber: http://suciantinovi.blogspot.co.id/2014/05/leftist-trie-and-hashing.html

Red Black Tree

Red Black Tree adalah BST dimana node-nodenya memiliki warna merah atau hitam. Warna inilah yang digunakan untuk menyeimbangkan tree nya. Dimana memiliki aturan seperti berikut:

• Setiap node mempunyai warna, antara merah atau hitam.
• Node root default nya warna hitam.
• Node external default nya warna hitam.
• Jika suatu node berwarna merah mempunyai children, maka harus berwarna hitam dua-duanya, tidak boleh merah.
• Node yang baru di insert berwarna merah.

Seperti BST, Red Black tree memiliki operasi seperti Insertion, Deletion dll. Setelah operasi dilakukan maka harus di ubah melalui single-rotation dan double-rotation agar memenuhi aturan.

3-2 Tree

2-3 Tree adalah salah satu tipe struktur data, dimana setiap node dengan anaknya, memiliki 2 children dan 1 elemen data (2 node) atau 3 children dan 2 elemen data (3 node). perlu diketahui, bahwa 2-3 Tree bukan Binary Tree.

Sifat-sifat 2-3 Tree

• Setiap non-leaf terdapat 2-node atau 3-node. Sebuah 2-node berisi satu item data dan memiliki dua anak/children (anak kiri dan anak tengah). Sebuah 3-node berisi dua item data dan memiliki 3anak/children (anak kiri, tengah, dan kanan).
• Semua leaf berada di level yang sama (level bawah/bottom level).
• Semua data yang disimpan akan diurutkan :
  1. Misalkan A adalah data yang tersimpan di 2-node. Subtree kiri harus berisi data yang nilainya lebih kecil dari A. Subtree tengah harus berisi data yang nilainya lebih besar dari A.
  2. Misalkan A dan B adalah data yang tersimpan di 3-node. Subtree kiri harus berisi data yang nilainya kurang dari A. Subtree tengah berisi nilai antara A dan B, dan subtree kanan berisi nilai yang lebih dari B.

Balanced Binary Search Tree terdiri dari 2 jenis, yaitu:

• AVL Tree
• Red Black Tree

Pada pertemuan kali ini, kami belajar AVL tree. AVL tree sendiri adalah binary search tree yang dapat menyeimbangkan tree nya sendiri. Tujuannya adalah untuk mempermudah searching.

Dalam AVL terdapat yang namanya balance factor. Balance factor ini adalah faktor keseimbangan antara child node kiri dan kanan. Dihitung dengan selisih antara child node kiri dan kanan. Jika tidak memiliki anak, maka dihitung 0. Balance factor pasti tidak lebih dari 1.

Lalu ada juga height factor. Dihitung dengan:

• Jika node root, tidak memiliki subtree, height factor = 0.
• Jika node adalah leaf, height factor = 1
• Jika node internal, height factor dihitung dari height tertinggi child node + 1.

To balance an AVL tree, we do these steps:

Single Rotation

Double Rotation